Answer:
D. 14 units.
Explanation:
We have been given coordinates of two points. We are asked to find the distance between both points.
We will distance formula to solve our given problem.
 , where,
, where,
 = Difference between two x-coordinates,
= Difference between two x-coordinates,
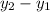 = Difference between two y-coordinates of same x-coordinates,
= Difference between two y-coordinates of same x-coordinates,
Let
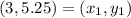 and
and
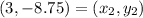 .
.
Upon substituting our given values in above formula, we will get:
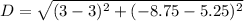
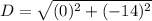
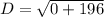

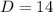
Therefore, the distance between the given points is 14 units and option D is the correct choice.