You can tell if two lines are parallel, perpendicular, or neither by looking at their slopes
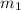 and
and
 :
:
- If
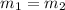 , i.e. if the two lines have the same slope, the lines are parallel
, i.e. if the two lines have the same slope, the lines are parallel - If
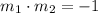 , the lines are perpendicular
, the lines are perpendicular - In all other cases, the lines are not parallel nor perpendicular.
Given two points
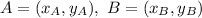 of a line, the slope is defined as the ratio between the y and x variation:
of a line, the slope is defined as the ratio between the y and x variation:
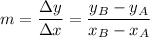
So in this case, we have
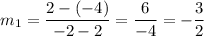
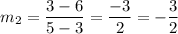
Since the two slopes are the same, the two lines are parallel.