Question

Point B is on line AC so that AB : BC = 2 : 1. Point D is on line AB so that AD : DB = 3 : 2. Find AD : DC

Answer 1

Firstly, we will draw figure

Let's assume

length of AC=x

we have

AB : BC = 2 : 1

so,

`AB=(2)/(3) x`

`BC=(1)/(3) x`

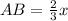
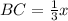
Point D is on line AB

and

`AB=(2)/(3) x`

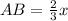
AD : DB = 3 : 2

so, we get

`AD=(3)/(5) *(2)/(3) x`

`AD=(2)/(5) x`

`DB=(2)/(5) *(2)/(3) x`

`DB=(4)/(15) x`

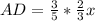
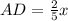
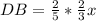
now, we can locate these values

Firstly, we will find DC

DC=DB+BC

now, we can plug values

`DC=(4)/(15) x+(1)/(3) x`

`DC=(3x)/(5)`

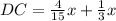
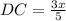
we have got

`AD=(2)/(5) x`

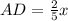
now, we can find ratio

`(AD)/(DC) =((2)/(5) x)/((3x)/(5))`

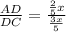
now, we can simplify it

`(AD)/(DC) =(2)/(3)`

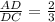
so,

AD:DC=2:3...........Answer