First we have to determine the time for the bag fall by the kinematic equation,
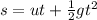
Here, u is initial velocity which is zero, g is acceleration due to gravity its value is 9.8 m/s2 and s is displacement and its value is given 30 m.
Therefore,
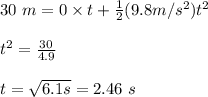
As sound travels at 340 m/s, so the time for the sound to travel back up the well,
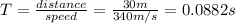
Thus , the splash is heard at
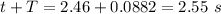 .
.
Therefore, splash is heard about 2.55 s after the bag is dropped.