we are given
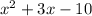
it's factor as (x+p)(x+q)
so, we can write as
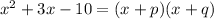
we can simplify it
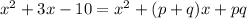
now, we can compare both sides
coefficient of x must be equal
so, we get

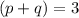
now, we can look at the table where p+q =3
so, we can see that when p+q=3 .... then p=-2 and q=5
so, option-A.......Answer