Question

In isosceles △ABC (AC = BC) with base angle 30° CD is a median. How long is the leg of △ABC, if sum of the perimeters of △ACD and △BCD is 20 cm more than the perimeter of △ABC?

Answer 1

Note necessary facts about isosceles triangle ABC:

• The median CD drawn to the base AB is also an altitude to tha base in isosceles triangle (CD⊥AB). This gives you that triangles ACD and BCD are congruent right triangles with hypotenuses AC and BC, respectively.
• The legs AB and BC of isosceles triangle ABC are congruent, AC=BC.
• Angles at the base AB are congruent, m∠A=m∠B=30°.

1. Consider right triangle ACD. The adjacent angle to the leg AD is 30°, so the hypotenuse AC is twice the opposite leg CD to the angle A.

AC=2CD.

2. Consider right triangle BCD. The adjacent angle to the leg BD is 30°, so the hypotenuse BC is twice the opposite leg CD to the angle B.

BC=2CD.

3. Find the perimeters of triangles ACD, BCD and ABC:

`P_(ACD)=AC+CD+AD=2CD+CD+AD=3CD+AD;`

`P_(BCD)=BC+CD+BD=2CD+CD+AD=3CD+AD;`

`P_(ABC)=AC+BC+AB=2CD+2CD+AD+BD=4CD+2AD.`

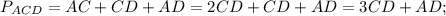
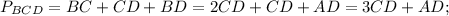
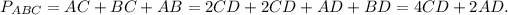
4. If sum of the perimeters of △ACD and △BCD is 20 cm more than the perimeter of △ABC, then

`P_(ACD)+P_(BCD)=P_(ABC)+20,\\ \\3CD+AD+3CD+AD=4CD+2AD+20,\\ \\6CD+2AD=4CD+2AD+20,\\ \\2CD=20.`

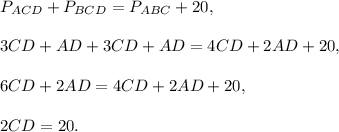
5. Since AC=BC=2CD, then the legs AC and BC of isosceles triangles have length 20 cm.

Answer: 20 cm.