Question

How many miles would it take for the two plans to be the same.

Answer 1

Let's assume

total miles is x

case-1:

initial fee is $ 65

additional rate is $0.20 per mile

so, the total cost = initial fee + x* additional rate

`C=65+0.20x`

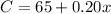
case-2:

initial fee is $ 0

additional rate is $0.70 per mile

so, the total cost = initial fee + x* additional rate

`C=0+0.70x`

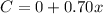
Since, both costs are same

so, we can set them equal

and we get

`65+0.20x=0+0.70x`

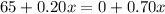
now, we can solve for x

`65=0.70x-0.20`

`65=0.50x`

`x=130`

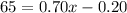
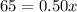
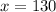
so, it would take 130 miles to drive for the two plans to cost the same .......Answer