Question

A subway train moving at 75 m/s begins to accelerate at a rate of -2.5 m/s squared for 5.0 seconds. It then travels at a constant speed for 100.0 seconds. It finally slows down to a stop at -5 m/s squared. Find the total distance covered and any other values needed to determine the total distance.

Answer 1

For the first 5.0 seconds of its motion, the train covers a distance of

`\left(75\,(\mathrm m)/(\mathrm s)\right)(5.0\,\mathrm s)+\frac12\left(-2.5\,(\mathrm m)/(\mathrm s)\right)(5.0\,\mathrm s)^2=344\,\mathrm m`

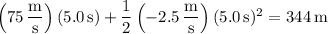
After the first 5.0 seconds, the train's velocity is

`75\,(\mathrm m)/(\mathrm s)+\left(-2.5\,(\mathrm m)/(\mathrm s^2)\right)(5.0\,\mathrm s)=62.5\,(\mathrm m)/(\mathrm s)`

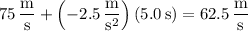
For the next 100.0 seconds, the trains covers a distance of

`\left(62.5\,(\mathrm m)/(\mathrm s)\right)(100.0\,\mathrm s)=6250\,\mathrm m`

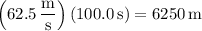
and thus a total distance of 6594 meters.

After the first 105.0 seconds, the train's velocity
`v` at time
`t` (where
`t=0` corresponds to the 105.0 second mark) is given by

`v(t)=62.5\,(\mathrm m)/(\mathrm s)+\left(-5\,(\mathrm m)/(\mathrm s^2)\right)t`

and its position
`x` at time
`t` (again,
`t=0` corresponds to the 105.0 second mark) by

`x(t)=\left(62.5\,(\mathrm m)/(\mathrm s)\right)t+\frac12\left(-5\,(\mathrm m)/(\mathrm s^2)\right)t^2`

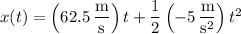
The time it takes for the train to stop is such that
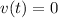`v(t)=0`, for which we have

`0=62.5\,(\mathrm m)/(\mathrm s)+\left(-5\,(\mathrm m)/(\mathrm s^2)\right)t\implies t=12.5\,\mathrm s`

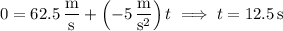
Then the distance covered in the final slow-down phase of the train is

`x(12.5\,\mathrm s)=391\,\mathrm m`

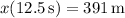
giving a total distance covered of about 6990 meters.