Question

A spring loaded toy shoots straight upward with a velocity of 4.5 m/s. Determine the maximum height it reaches. Determine the time it takes to return to its initial position. Determine the velocity of the toy if it falls 1.0m below where it is launched from. Please help me with this problem.

Answer 1

Recall that

`{v_y}^2-{v_(0y)}^2=2a_y(y-y_0)`

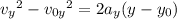
At its maximum height
`y_{\mathrm{max}}`, the toy will have 0 vertical velocity, so that

`-\left(4.5\,(\mathrm m)/(\mathrm s)\right)^2=2\left(-9.8\,(\mathrm m)/(\mathrm s^2)\right)y_{\mathrm{max}}`

`\implies y_{\mathrm{max}}=1.0\,\mathrm m`

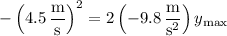
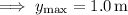
For the toy to reach this maximum height, it takes time
`t` such that

`\frac{0+v_0}2t=y_{\mathrm{max}}\implies t=0.46\,\mathrm s`

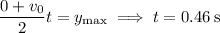
which means it takes twice this time, i.e.
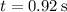`t=0.92\,\mathrm s`, for the toy to reach its original position.

The velocity of the toy when it falls 1.0 m below its starting point is

`{v_y}^2-\left(4.5\,(\mathrm m)/(\mathrm s)\right)^2=2\left(-9.8\,(\mathrm m)/(\mathrm s^2)\right)(0-1.0\,\mathrm m)`

`\implies{v_y}^2=39.85\,(\mathrm m^2)/(\mathrm s^2)`

`\implies v_y=-6.4\,(\mathrm m)/(\mathrm s)`

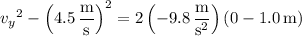
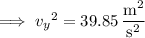
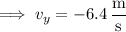
where we took the negative square root because we expect the toy to be moving in the downward direction.