Question

Consider the linear equation g(x) = −f(x + 3) − 2. Choose True or False for each statement.

A. When compared to f(x) = x2, g(x) will
have a vertical stretch of 3.
A True B False
B. When compared to f(x) = x2, g(x) will be
reflected over the x-axis.
A True B False
C. When compared to f(x) = x2, g(x) will be
translated left 3 units, and down 2 units.
A True B False

Answer 1

we are given

`g(x)=-f(x+3)-2`

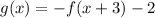
we will check each options

(A)

`f(x)=x^2`

now, we can find g(x)

`g(x)=-(x+3)^2-2`

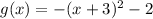
Since, it is not multiplied to f(x) by 3

so, it is not vertical stretch by 3 units

so, this is FALSE

(b)

`f(x)=x^2`

now, we can find g(x)

`g(x)=-(x+3)^2-2`

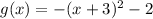
Since, it is -1 multiplied to f(x)

so, it is reflected about x-axis

so, this is TRUE

(c)

`f(x)=x^2`

now, we can find g(x)

`g(x)=-(x+3)^2-2`

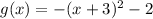
Since, there is (x+3)^2

so, it shifted left side by 3 units

and it is -(x+3)^2 -2

2 is subtracted

so, it is down by 2 units

so, this is TRUE