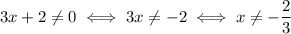Question

Given: g(x)=1/x+2 and h(x)=3x Check all restrictions on the domain of gOh.

1. x does not equal 0
2. x does not equal -2
3. x does not equal -2/3
4. there are no restrictions

Answer 1

x not equal to -2/3 is the answer.

Answer 2

The composite function
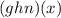`(g \circle h)(x)` works like this:

• Take a number
  `x` as input
• Evaluate h(x) = 3x. Let's call this output z.
• Evaluate g(x) = 1/(z+2)

So, if we substitute back z = 3x, the final output is 1/(3x+2). We know that the denominator of a fraction can't be zero, so we must impose

`3x+2 \\eq 0 \iff 3x \\eq -2 \iff x \\eq -(2)/(3)`