Let's assume P2 point be (a,b)
P2=(a,b)
The midpoint of the line segment from P1 to P2 is (-6,5)
P1=(-9,7)
so, firstly, we will find mid-point between P1 and P2
we get
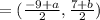
now, this point must be (-6,5)
so, we can set it equal
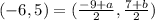
now, we can compare x-values and y-values
we get
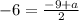
we can solve for a
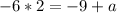
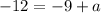
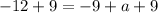
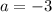
now, we can compare y-value
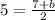
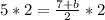
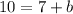
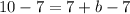
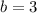
so, we will get
P2=(a,b)
P2=(-3,3)...............Answer