Question

Let line L1 be the graph of 5x + 8y = -9. Line L2 is perpendicular to line L1 and passes through the point (10,10). If line L2 is the graph of the equation y=mx +b, then find m+b.

Answer 1

-22/5.

Explanation:

hope this helps

Answer 2

• Slope-Intercept Form: y = mx + b, with m = slope and b = y-intercept

So firstly, remember that perpendicular lines have slopes that are negative reciprocals to each other. To find the slope of L1, the easiest method is to convert it into slope-intercept form.

Firstly, subtract 5x on both sides of the equation:
`8y=-5x-9`

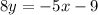
Next, divide both sides of the equation by 8 and your slope-intercept form will be
`y=-(5)/(8)x-(9)/(8)`

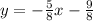
Now looking at this equation, the slope appears to be -5/8 for L1. Since L2 is perpendicular, this means that the slope of L2 is 8/5.

Next, to find the y-intercept, put the slope into the m variable and put (10,10) into the x and y placeholders to solve for b as such:

`10=(8)/(5)*10+b\\10=16+b\\-6=b`

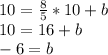
Putting it together, your equation is
`y=(8)/(5)x-6`, with m = 8/5 and b = -6.

Next, to find the sum you first need to convert -6 so that it has a denominator of 5. To do this, multiply -6 by 5/5 as such:

`-(6)/(1)*(5)/(5)=-(30)/(5)`

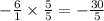
Next, add the numerators together:

`-(30)/(5)+(8)/(5)=-(22)/(5)`

Your final answer is -22/5.