Question

(-3/5, 7/5) and (2/5, 6/5)

A. The equation of the line in slope-intercept form is ?
B. Standard Form
Please help

Answer 1

First, let's find the slope of the line using the formula
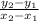`(y_2 - y_1)/(x_2 - x_1)`, where
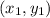`(x_1, y_1)` and
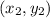`(x_2, y_2)` are points on the line.

The equation for the slope of this line would be:

`((7)/(5) - (6)/(5))/(-(3)/(5) - (2)/(5)) = ((1)/(5))/(-1) = -(1)/(5)`

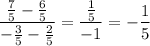
Now, let's find use the point-slope equation to find an equation for our line, which is
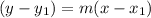`(y - y_1) = m(x - x_1)`, where
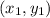`(x_1, y_1)` is a point on the line and
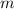`m` is the slope. The point-slope equation for our line would be:

`(y - (6)/(5)) = -(1)/(5)(x - (2)/(5))`

`y - (6)/(5) = -(1)/(5)x + (2)/(25)`

`y = -(1)/(5)x + (32)/(25)`

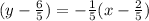
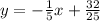
The slope-intercept form of the line would be y = -x/5 + 32/25.

Now, we can use operations to convert this equation into standard form:

`25y = -5x + 32`

`5x + 25y = 32`

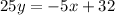
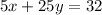
The standard form of the line would be 5x + 25y = 32.