Question

Given: △ABC, m∠C=90° m∠ABC=30°, AL ∠ bisector CL=6 ft. Find: LB

Answer 1

12ft

Explanation:

30 60 90 rule

Answer 2

For a better understanding of the solution given here please go through the diagram in the file attached.

To solve this question we will make use of the "Triangle Angle Bisector Theorem", which states that, "An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle."

Thus, in our question, we will have:

`(LB)/(CL)= (AB)/(AC)`

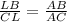
The above equation can be rearranged as:

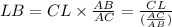`LB=CL* (AB)/(AC)=(CL)/(((AC)/(AB)))`...(Equation 1)

If we have a proper look at the denominator which is
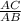`(AC)/(AB)`, we note that in
`\Delta ABC`,
`(AC)/(AB)=Sin(\angle ABC)=Sin(30^\circ)`

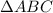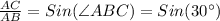
Thus, (Equation 1) wil give us:

`LB=(CL)/(Sin(30^\circ)) =(6)/(0.5)=12`

Therefore, LB= 12 feet