Question

suppose HJ is on s coordinate plane located at H(-5,2) and J(1,4). Under a dilation centered at(3,2), HJ becomes H'J' with coordinates H'(-1,2) and J'(2,3). What is the scale factor for this dilation?

Answer 1

Suppose HJ is on s coordinate plane located at H(-5,2) and J(1,4). Under a dilation centered at(3,2), HJ becomes H'J' with coordinates H'(-1,2) and J'(2,3). What is the scale factor for this dilation?

Answer 2

Scale factor = 1/2

Explanation:

Distance formula:

`Distance=√((x_2-x_1)^2+(y_2-y_1)^2)`

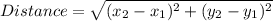
It is given that on a coordinate plane two points are located at H(-5,2) and J(1,4).

Using distance formula we get

`HJ=√((1-(-5))^2+(4-2)^2)\Rightarrow √(36+4)=√(40)\Rightarrow 2√(10)`

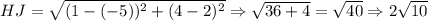
After dilation HJ becomes H'J' with coordinates H'(-1,2) and J'(2,3).

`H'J'=√((2-(-1))^2+(3-2)^2)\Rightarrow √(9+1)=√(10)`

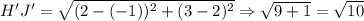
Scale factor of dilation is

`\text{Scale factor}=\frac{\text{Length of segment of image}}{\text{Length of corresponding segment of preimage}}`

`\text{Scale factor}=(H'J')/(HJ)`

`\text{Scale factor}=(√(10))/(2√(10))`

`\text{Scale factor}=(1)/(2)`

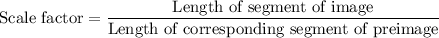
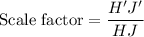
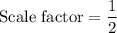
Therefore, the scale factor is 1/2.