Question

An apartment building has eight floors. if seven people get on the elevator on the first floor, what is the probability they all want to get off on different floors

Answer 1

We have been given that there are total 8 floors and 7 people get on the elevator on the first floor.

Therefore, the total number of possible outcomes are
`7^7`

Now, on the second floor any person can get off. So there are total 7 possibilities for second floor.

Now, since 1 person is already get off in the second floor, so on the third floor there are 7 possibilities.

Similarly, for

fourth - 5 possibilities

fifth - 4 possibilities

sixth- 3 possibilities

seventh - 2 possibilities

eight - 1 possibility

Therefore, the required probability is given by

`P(E)=(n(E))/(n(S)) \\ \\ P(E)= (7 * 6  * 5  * 4  * 3  * 2  * 1)/(7^7) \\ \\ P(E)=(5040)/(823543) \\ \\ P(E)=0.00612`

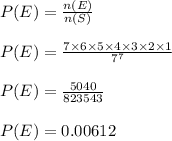
Therefore, the probability is 0.00612