Question

Let r be the region bounded by y = x 2 and y = 9. find a and b so that the horizontal lines y = a and y = b split the region r into 3 pieces of equal area.

Answer 1

y = x² has a lower bound at the vertex (0, 0); y = 0

y = 9 has an upper bound at y = 9

x² = 9 ⇒ x = +/- 3 the region is bounded on the left at x = -3 and on the right at x = 3

Solve the integral from -3 to 3 to find the area under the curve, then multiply by 1/3 to calculate 1/3 of the area.

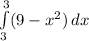`\int\limits^3_3 (9 - {x^(2)}) \, dx` = (9x - x³/3) | from -3 to 3

= (9(3) - 3³/3) - (9(-3) - (-3)³/3)

= (27 - 9) - (- 27 - (-9))

= 16 - (-16)

= 32

*** 32/3 is 1/3 of the area ****

Now that we know what 1/3 of the area is, we can find the height at y = a which will satisfy 1/3 of the area. We do this by solving the integral from "0 to a" and setting it equal to 1/3 of the area (32/3).

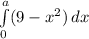`\int\limits^a_0 (9 - {x^(2)}) \, dx` - a(9 - a²)

= (9x - x³/3) | from 0 to a - (9a - a³)

= (9a - a³/3) - (9(0) - (0)³/3) - 9a + a³

= 9a - a³/3 - 9a + a³

= a³ - a³/3

= 2a³/3

32/3 = 2a³/3

32 = 2a³

16 = a³

∛16 = a

2∛2 = a (This is the distance from the upper bound (y = 9)

Answer: y = 9 - 2∛2

Follow the same steps using 2/3 of the area (64/3) to find "b".

64 = 2b³

32 = b³

∛32 = b 3.17

2∛4 = b (This is the distance from the upper bound (y = 9)

Answer: y = 9 - 2∛4