Question

College LEVEL can you help me? :S

Answer 1

Although the formula looks involved, the key here is looking to see where the information goes.

We are given all the pieces but need to convert mph to ft/s to use the formula. Let's do it with 1 mph so that we have a ratio to use. We and solve a unit conversion problem.

`(1mile)/(hour) * (hour)/(60 minutes) * (minute)/(60 seconds) * (5280 feet)/(mile) = (5280)/(60*60) = (5280)/(3600) = 1.46666`

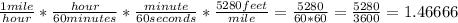
That ratio tells us that 1 mph is 1.466666 ft/s. Now we solve two proportions.

1 mph / 1.466666 feet per second = 60 mph / x feet per second.

1x = (60)(1.466666)

So x = 88 feet per second.

Next, We repeat for 24 mph.

1 mph / 1.46666 feet per second = 24 mph / x feet per second.

1x = (1.4666666)(24)

x = 35.2 feet per second

Now we have the found appropriate V₁ and V₂. V₁ > V₂, so V₁ is 88 ft/s and V₂ is 35.2 ft/s. The problem tells us θ = 2.3 degrees, K₁ = .4 and K₂ = .06. The rest of the problem is calculator work. Start by substituting our degree measure of 2.3 degrees and the given values in the problem for V₁, V₂, K₁, and K₂

`D = (1.05[(88)^(2)-(35.2)^(2)])/(64.4(.4+.06 + (sin 2.3)))`

`D = (1.05[(7744-1239.04])/(64.4(.46 + (sin 2.3)))`

`D = (1.05(6504.96))/(64.4(.46 + 0.04013))`

`D = (6830.208)/(64.4(0.50013))`

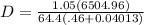
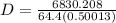
D = 6830.208 / 32.208372

D = 212.0631 = 212 (to the nearest foot)

Thus the car needs 212 feet to stop.