Question

ANSWER FOR 25 POINTS!!!

Carlos graphed the system of equations that can be used to solve x^3 - 2x^2 + 5x - 6 = -4x^2 + 14x + 12

What are the roots of the polynomial equation?

A) –3, –2, 3

B) –3, 2

C) 18, 32

D) 18, 32, 66

Answer 1

Answer: Option 'A' is correct.

Explanation:

Since we have given that

Systems of two equations :

`x^3 - 2x^2 + 5x - 6\ and-4x^2 + 14x + 12`

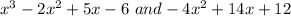
And according to question, we have

`x^3 - 2x^2 + 5x - 6 = -4x^2 + 14x + 12`

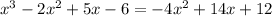
We can see from the graph that "The two equations are intersected at "

`x=-3,x=-2,x=3`

and if simplify the above equations, we get,

`x^3 - 2x^2 + 5x - 6 = -4x^2 + 14x + 12\\\\x^3-2x^2+5x-6+4x^2-14x-12=0\\\\p(x)=x^3+2x^2-9x-18`

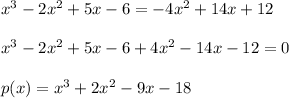
But the roots will be same as above as they both get intersected at these points only,and

`p(-3)=-27+18+27-18=0\\\\p(-2)=-8+8+18-18=0\\\\p(3)=27+18-27-18=0`

`-3,-2\ and\ 3\text{ are the roots of the polynomial equation}`

Hence, Option 'A' is correct.

Answer 2

Carlos graphed two graphs:
`y=x^3 - 2x^2 + 5x - 6` and
`y=-4x^2 + 14x + 12.`

As you can see from the diagram, these two curves have three common points at x=-3, x=-2 and x=3.

These three points ae solutions of the equation
`x^3 - 2x^2 + 5x - 6 = -4x^2 + 14x + 12.`

Answer: correct choice is A.