Hello!
Applying the base 10 logarithmic properties, we have:
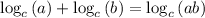
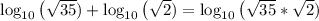
If we have:
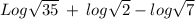
So:

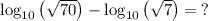
Applying the base 10 logarithmic properties, we have:
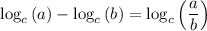
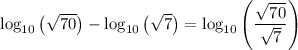
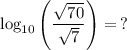
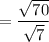
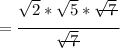
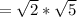
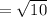
So:
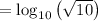
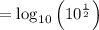
Applying the base 10 logarithmic properties, we have:
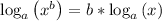
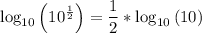
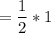

___________________________
I Hope this helps, greetings ... DexteR! =)