Question

Marty and Ethan both wrote a function, but in different ways.

Marty
y+3=1/3(x+9)

Ethan
x y
-4 9.2
-2 9.6
0 10
2 10.4

Whose function has the larger slope?

1. Marty’s with a slope of 2/3
2. Ethan’s with a slope of 2/5
3. Marty’s with a slope of 1/3
4. Ethan’s with a slope of 1/5

Answer 1

Marty’s with a slope of 1/3

Explanation:

Marty

y+3=(1/3)*(x+9)

y + 3 = (1/3)*x + 3

y = (1/3)*x

Marty's slope: 1/3

To calculate Ethan’s slope we use the following formula :

m = (y2 - y1)/(x2 - x1)

where (x1, y1) and (x2, y2) are points of the function. Replacing with points (0,10) and (2, 10.4) we get:

m = (10.4 - 10)/(2 - 0) = 1/5

Ethan’s slope: 1/5

Answer 2

Option 3 is correct

Marty’s with a slope of 1/3

Explanation:

Using slope intercept form:

The equation of line is:
`y=mx+b` ....[1]

where,

m is the slope and b is the y-intercept.

Formula for Slope is given by:

`\text{Slope} = (y_2-y_1)/(x_2-x_1)` ....[2]

As per the statement:

Marty and Ethan both wrote a function, but in different ways.

Marty equation is:

`y+3 = (1)/(3)(x+9)`

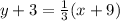
using distributive property
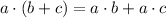`a \cdot(b+c) = a\cdot b + a\cdot c` we have;

`y+3 = (1)/(3)x+3`

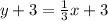
Subtract 3 from both sides we have;

`y= (1)/(3)x`

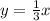
On comparing with [1] we have;

Slope of Marty =
`(1)/(3)=0.333..`

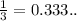
Ethan wrote a function:

Consider any two values from the table we have;

(0, 10) and (2, 10.4)

Substitute these in [2] we have;

`\text{Slope} = (10.4-10)/(2-0)=(0.4)/(2) =0.2`

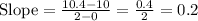
Slope of Ethan = 0.2

`\text{Slope of Ethan} < \text{Slope of Marty}`

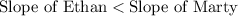
Therefore, . Marty’s with a slope of 1/3 function has the larger slope