Answer:
The probability of rolling a 6 on the number cube and the coin landing on heads is:
fraction 1,107 over 10,000 i.e.
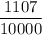
Explanation:
Let A denote the event of rolling a 6 on number cube.
and B denote the event of landing a head on a coin.
Clearly both the events A and B are independent.
Also, let P denote the probability of an event.
We are asked to find: P(A∩B)
We know that when two events A and B are independent.
Then,

Now, based on the two tables we have:

( Since, 6 comes up on rolling a number cube 27 times out of a total of 100 times)
Also,
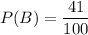
( since head comes up 41 times out of a total of 100 times)
Hence, we get:
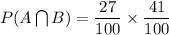
i.e.
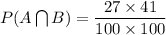
i.e.
