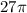Question

Find the length of arc ABC. Express answer in terms of pi. PC=18in

Answer 1

The formula would be 2 * pi * (central angle)/360

Hence, 2 * 22/7 * 270/360 => 84.823 in.

Answer 2

Answer:
`27\pi`

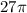
Explanation:

In the given figure we have given a circle in with radius PC = 18 inches

Also, the central angle made by arc AC
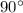`90^(\circ)` or
`(\pi)/(2)`

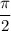
Since the sum of angles at a point is
`2\pi`

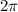
Then , the central angle made by arc AC :-

`\theta=2\pi-(\pi)/(2)=(3\pi)/(2)`

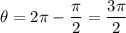
The formula to find the arc length is given by :-

`l=r\theta`

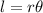
Then the length of arc ABC will be :-

`l=(18)((3\pi)/(2))=27\pi`

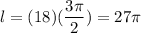
Hence, the length of arc ABC =
`27\pi`