The given expression is
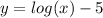
And log cant gives the value of negative number or 0. THerefore x must be greater then 0. THat is
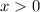
So the domain is
 Range.
Range.
To find the range, we have to first find the inverse of the given function. And domain of the inverse function is the range of the given function.
So to find the inverse, first we switch x and y, and then solve for y. That is
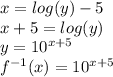
And there is no restriction on x. SO the domain of the inverse function is all real numbers. And hence the range of the inverse function is all real numbers.
Correct option is the first option .