Question

Solve (x + 4)2 – 3(x + 4) – 3 = 0 using substitution.

u = ___

A. x
B. x + 4
C. 3(x + 4)
D. (x + 4)^2
please show a little bit of work so i know your answer isn't BS

Answer 1

I would say that the answer is B

Answer 2

Option B is correct.

u= x+4

Explanation:

Solve the equation:

`(x+4)^2-3(x+4)-3 = 0`

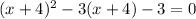
Using substitution:

Let u = x+4

then;

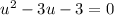`u^2-3u-3=0` ....[1]

For a quadratic equation
`ax^2+bx+c = 0` ....[2], then the solution is given by:

`x = (-b \pm √(b^2-4ac))/(2a)`

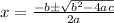
On comparing equation [1] and [2] we have;

a = 1 , b = -3 and c = -3

then;

`u= (-(-3) \pm √((-3)^2-4(1)(-3)))/(2(1))`

⇒
`u= (3 \pm √(9+12))/(2)`

⇒
`u= (3 \pm √(21))/(2)`

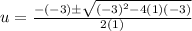
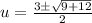
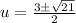
Substitute u = x+4

then;

⇒
`x+4= (3 \pm √(21))/(2)`

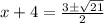
Subtract 4 from both sides we have;

`x= (3 \pm √(21))/(2) - 4= (3 \pm √(21)-8)/(2)`

⇒
`x= (3 + √(21)-8)/(2)= (-5 + √(21))/(2)`

and

`x= (3 - √(21)-8)/(2)`

⇒
`x= (-5 - √(21))/(2)`

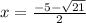
Therefore, the solution for the given equation are,

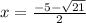`x= (-5 - √(21))/(2)` ,
`(-5 + √(21))/(2)`