Question

Solve the following quadratic equation by the square root property of equality. (x - 8)^2 = 48

Answer 1

Solve for x over the real numbers by completing the square.

(x - 8)² = 48

Take the square root of both sides:

x - 8 = 4 √(3) or x - 8 = -4 √(3)

Add 8 to both sides:

x = 8 + 4 √(3) or x - 8 = -4 √(3)

Add 8 to both sides:

Answer: x = 8 + 4 √(3) or x = 8 - 4 √(3)

Answer 2

Answer: The required solution of the given equation is

`x=8+4\sqrt3,~~8-\sqrt3.`

Step-by-step explanation: We are given to solve the following quadratic equation by the square root property of equality :

`(x-8)^2=48~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

Using the square root property of equality, we have from equation (i) after taking the square roots on both sides that

`x-8=\pm√(48)\\\\\Rightarrow x-8=\pm√(16*3)\\\\\Rightarrow x-8=\pm4\sqrt3\\\\\Rightarrow x=8\pm4\sqrt3.`

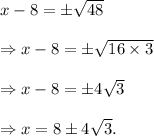
Thus, the required solution of the given equation is

`x=8+4\sqrt3,~~8-\sqrt3.`