Question

A right triangle (triangle 1) has measurements of a = 505 mm and b = 286 mm. What are the measurements for c, α, and β?

Answer 1

In a right triangle with a = 505 mm and b = 286 mm, the length of c is approximately 579.70 mm. The measures of the angles α and β are approximately 29.47° and 30.53°, respectively.

Step-by-step explanation:

In the given right triangle, let a = 505 mm and b = 286 mm. We can use the Pythagorean theorem to find the length of the hypotenuse (c) and the measures of the two non-right angles (α and β).

Using the Pythagorean theorem, a² + b² = c², we can substitute the given values to find c.

c² = 505² + 286²

c² = 254025 + 81856

c² = 335881

c = √335881

c ≈ 579.70 mm

To find the measures of the angles α and β, we can use the trigonometric functions sine and cosine.

Sine of α = b/c

Sine of α = 286/579.70 ≈ 0.4946

α ≈ arcsin(0.4946)

α ≈ 29.47°

Cosine of α = a/c

Cosine of α = 505/579.70 ≈ 0.8691

β ≈ arccos(0.8691)

β ≈ 30.53°

Answer 2

see the attached figure to better understand the problem

Step 1

Find the value of c

we know that

Applying the Pythagorean Theorem

`c^(2) =a^(2)+b^(2)`

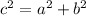
we have

`a=505\ mm`

`b=286\ mm`

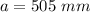
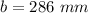
substitute the values in the formula

`c^(2) =505^(2)+286^(2)`

`c^(2) =336,821`

`c=580.36\ mm`

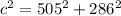
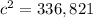
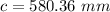
Step 2

Find the value of angle A (α)

we know that

in the right triangle ABC

`cos(A)=(b)/(c) \\ \\cos(A)=(286/580.36)\\ \\A=arc\ cos(286/580.36)\\ \\A=60.48\ degrees`

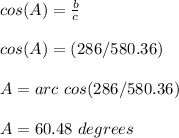
Step 3

Find the angle B (β)

we know that

in the right triangle ABC

angle A and angle B are complementary angles

so

A+B=90

solve for B

B=90-A-------> B=90-60.48-----> B=29.52°

therefore

the answers are

a) the measure of side c is 580.36 mm

b) the measure of the angle α is 60.48°

c) the measure of the angle β is 29.52°