Question

There are two major tests of readiness for college: the act and the sat. act scores are reported on a scale from 1 to 36. the distribution of act scores in recent years has been roughly normal with mean μ = 20.9 and standard deviation σ = 4.8. sat scores are reported on a scale from 400 to 1600. sat scores have been roughly normal with mean μ = 1026 and standard deviation σ = 209. joe scores 1351 on the sat. assuming that both tests measure the same thing, what score (±1) on the act is equivalent to joe's sat score? .

Answer 1

Solution: We are given:

ACT scores follow normal distribution with
`\mu=20.9,\sigma =4.8`

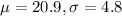
SAT scores follow normal distribution with
`\mu=1026,\sigma=209`

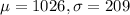
Now, let's find the z score corresponding to Joe's SAT score 1351.

`z=(x-\mu)/(\sigma)`

`=(1351-1026)/(209)`

`=(325)/(209)`

`=1.56`

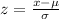
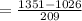
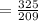
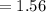
Therefore, Joe's SAT score is 1.56 standard deviations above the mean.

Now, we have find the Joe's ACT score, which will be 1.56 standard deviations above the mean.

Therefore, we have:

`z=(x-\mu)/(\sigma)`

`1.56=(x-20.9)/(4.8)`

`1.56 * 4.8 = x - 20.9`

`7.488=x-20.9`

`x=20.9+7.488`

`x=28.388 \approx 28.4`

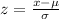
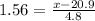
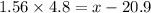
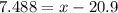
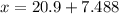
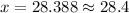
Therefore, Joe's equivalent ACT score to SAT score 1351 is 28.4