Question

Answer a 30.0 kg shell is fired from a 2,000 kg cannon with a velocity of 500 m/s. what is the resulting velocity of the cannon?

Answer 1

It is
`7.5(m)/(s)` in the same direction of the shell's velocity but in the opposite sense.

Step-by-step explanation:

In order to calculate the velocity of the cannon, we are going to use the Momentum Conservation Law.

If the exterior resultant force acting over a particles system is nule therefore the momentum is constant.

We can calculate the momentum as

`p=m.v`

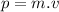
Where ''p'' is the momentum (a vectorial magnitude)

Where ''m'' is the mass of the object

And where ''v'' is the velocity (a vectorial magnitude)

In the exercise, the momentum is constant (because the exterior resultant force is equal to zero).

So we can write :

`m1.v1=m2.v2` (I)

Where m1 is the mass of the shell

Where v1 is the velocity of the shell

Where m2 is the mass of the cannon

And where v2 is the velocity of the cannon.

Replacing all the data in the equation (I) :

`(30kg).(500(m)/(s))=(2000kg).v2`

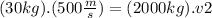
If we solve to find v2 :

`v2=((30kg).(500(m)/(s)))/(2000kg)=7.5(m)/(s)`

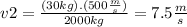
We find that the resulting velocity of the cannon is
`7.5(m)/(s)`

Answer 2

To calculate the resulting velocity of the cannon, we use the concept of conservation of momentum.

`m_(1)v_(1) =m_(2)v_(2)`

Here,
`m_(1)` is the mass of cannon and its value is 2000 kg,
`m_(2)` is the mass of the shell which is fired from cannon and its value is 30.0 kg,
`v_(2)` is the velocity of shell and
`v_(1)` is the resulting velocity of cannon.

Substituting these values in above formula we get,

`2000 kg * v_(1) =30.0 kg * 500 m/s\\\\\ v_(1) = (30.0 kg* 500 m/s)/(2000 kg) =  7.5 m/s`

The cannon recoil with velocity of 7.5 m/s.