Question

A daring ranch hand sitting on a tree limb wishes to drop vertically onto a horse galloping under the tree. the constant speed of the horse is 12.0 m/s, and the distance from the limb to the level of the saddle is 2.50 m. (a) what must be the horizontal distance between the saddle and limb when the ranch hand makes his move? m (b) how long is he in the air?

Answer 1

(a) The ranch hand must be at a distance of 8.57 m from the saddle when he makes his move.

(b) The time the ranch hand is in air is 0.714 s.

When the ranch hand drops down, he falls under gravity. He falls a distance equal to the distance of the limb from the saddle. Let the ranch hand take a time t to drop down.In the same time t, the galloping horse moving with a constant velocity, should cover the distance between itself and the tree limb.

Calculate the time taken by the ranch hand to drop down assuming he drops down with no initial velocity.

Use the equation of motion

`s=(1)/(2) gt^2`

Here, g is the acceleration due to gravity.

Substitute 2.50 m for s, 9.8 m/s² for g and calculate t.

`s=(1)/(2) gt^2\\ 2.50 m=(1)/(2)(9.8 m/s^2)t^2\\ t=0.714 s`

The distance d traveled by the horse during this time is given by,

`d=vt=(12.0 m/s)(0.714m)=8.57m`

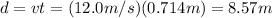
If the farm hand drops down when the horse is 8.57 m from him, he would be 0.714s in air and land on the saddle.