Question

Jamie needs to determine the distance across a river. She selects a rock, R, on the opposite river bank. She finds a tree, T, on her side of the river such that RT is perpendicular to the river. Next, Jamie walks 50 yards down the river from the tree, T, to a spot, C. Using a compass that she made from two sticks, she measures TCR. She

then walks from C in a direction that makes the same angle as TCR with the river bank on her side of the river. She keeps walking in that direction until she sees the tree and the rock in a straight line from her position. She marks this point B and then paces from B to T to measure the distance from point B to the tree. If BT turns out to be 75 yards, what is RT, the distance across the river?

Answer 1

Since RT is perpendicular to the river, you have that segment CT is perpendicular to RT and, thus, CT⊥RB, because point B lies in a straight line with points R and B. Angles TCR and TCB are congruent (she walks from C in a direction that makes the same angle as TCR with the river bank on her side of the river).

This means that triangle CRB is isosceles triangle with base BR and height CT, because height CT is also a bisector of angle BCR.

The height CT divides triangle BCR into two right triangles BCT and RCT, where:

• CT is common leg;
• ∠TCR≅∠TCB,

then by LA Theorem these two triangles are congruent (ΔBCT≅ΔRCT).

Congruent triangles have congruent corresponding sides:

• BC≅RC;
• CT≅CT;
• BT≅TR.

If BT turns out to be 75 yards, then TR=75 yards.

By the Pythagorean theorem,

`BC^2=CT^2+BT^2,\\ \\BC^2=50^2+75^2=2500+5625=8125,\\ \\BC=√(8125)=25√(13).`

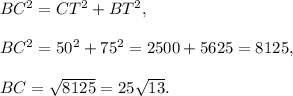
If
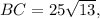`BC=25√(13),` then distance from the spot to the rock is
`CR=25√(13).`

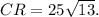
Answer: RT=75 yards,
`CR=25√(13)` yards.