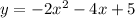Question

Can you help me im not that good at math and its a clear photo

y =___x^2+__x+______

Answer 1

• Vertex/General Form: y = a(x - h)^2 + k, with (h,k) as the vertex
• (x + y)^2 = x^2 + 2xy + y^2
• Standard Form: y = ax^2 + bx + c

So before I put the equation into standard form, I'm first going to be putting it into vertex form. Since the vertex appears to be (-1,7), plug that into the vertex form formula:

`y=a(x-(-1))^2+7\\y=a(x+1)^2+7`

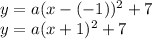
Next, we need to solve for a. Looking at this graph, another point that is in this line is the y-intercept (0,5). Plug (0,5) into the x and y placeholders and solve for a as such:

`5=a(0+1)^2+7\\5=a(1)^2+7\\5=a+7\\-2=a`

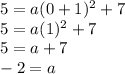
Now we know that our vertex form equation is y = -2(x + 1)^2 + 7.

However, we need to convert this into standard form still, and we can do it as such:

Firstly, solve the exponent:
`y = -2(x^2+2x+1) + 7`

Next, foil -2(x^2+2x+1):
`y = -2x^2-4x-2+7`

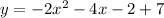
Next, combine like terms and your final answer will be:
`y = -2x^2-4x+5`