Final answer:
The perimeter of a rectangle with given dimensions can be found by substituting the value of the length into the width expression and then using the formula 2 * (length + width).
Step-by-step explanation:
Your question seems to relate to the concept of finding the perimeter of a rectangle. The perimeter of a rectangle is determined by doubling the sum of the length and width. If a rectangle has a length of x and a width of
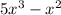 , and we know the length is 5 feet, we can find the perimeter by plugging in the value of x into the expression for the width. However, there seems to be an issue with the width's expression; there should be an operator between
, and we know the length is 5 feet, we can find the perimeter by plugging in the value of x into the expression for the width. However, there seems to be an issue with the width's expression; there should be an operator between
 Assuming there's a typo, let's consider the width is correctly written as
Assuming there's a typo, let's consider the width is correctly written as
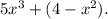
To find the width, replace 'x' with '5':
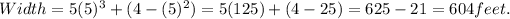
Then, compute the perimeter:
Perimeter = 2 * (length + width) = 2 * (5 + 604) = 2 * 609 = 1218 feet.
This gives us the perimeter of the rectangle when the length is 5 feet.