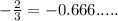Answer:
The repeating decimal number is
Explanation:
Given : Numbers
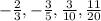
To find : Which number below represents a repeating decimal ?
Solution :
To determine the repeating decimal we have to solve each fraction,
i.e. divide denominator by numerator if we get the reminder 0 it is terminating but if remainder is not zero and quotient remain same then it is repeating.
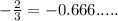
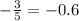
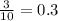
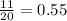
Therefore, The repeating decimal number is