Question

What is 456/123 as a repeating decimal using bar notation?(can use calculator, but show work)

PLS HELP DUE TOMORROW

Answer 1

The answer is 3.70731 with the bar notation over 70731

Explanation:

The definition of a repeating or recurring decimal is decimal representation of a number whose digits are periodic (repeating its values at regular intervals). For example:

`(1)/(3) = 0.3333333...`

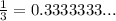
where the 3 is the repeating decimal. And can be expressed as shown in the picture,

`(7)/(11) = 0.636363...`

where the 63 are the repeating decimals. And can be expressed as shown in the picture,

`(1)/(7) = 0.142857142857...`

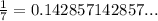
where the 142857 are the repeating decimals. And can be expressed as shown in the picture,

Therefore, our fraction is:

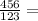`(456)/(123) =` 3.7073170731

where the 70731 are the repeating decimals.

Answer 2

A repeating decimal is a decimal fraction in which a figure or group of figures is repeated indefinitely, as in 0.666… or as in 1.851851851….

As the given number is 456/123 ,

So in repeating decimal it can be written as

`(456)/(123) = 3.707317073170731.........`

So with bar notation, it will be written as

3. 70731 with bar notation sign over 70731