Question

A rectangle is a four sided flat shape where every interior is a right angle. Therefore, opposite sides are parallel and consecutive sides are perpendicular. Rae is drawing rectangle PQRS on a coordinate plane. The rectangle has cord images P(-1,2), Q(2,4), R(x,y), and S(3,-4).

Answer 1

The coordinates for point R will be (-1, -6). This is because a rectangle has opposite sides and as you plot your rectangle with these defines points along with that of R, you will be able to successfully achieve a perfect rectangle.

Answer 2

coordinates of R(x,y) is R(6,-2).

Explanation:

We have given the coordinates of rectangle PQRS as: P(-1,2), Q(2,4), R(x,y), and S(3,-4).

We know the slope formula:

Slope =
`(y_2-y_1)/(x_2-x_1)`

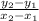
Now, by applying slope formula

Slope of PQ =
`(4-2)/(2-(-1))`

=
`(2)/(3)`

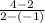
Slope of RS =
`(-4-y)/(3-x)`

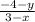
Slope of QR =
`(y-4)/(x-2)`

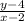
We know that, slopes of PQ and RS are equal because these are parallel to each other.

Slope of PQ = Slope of RS

`(2)/(3)` =
`(-4-y)/(3-x)`

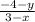
2(3-x) = 3(-4-y)

6-2x = -12-3y

2x-3y = 18...........equation(1)

Slopes of perpendicular lines are negative reciprocal. Therefore,

Slope of PQ =
`(-1)/(slope \ of \ QR)`

`(2)/(3)` =
`(-1)/((y-4)/(x-2) )`

`(2)/(3)` =
`(-x+2)/(y-4)`

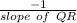
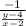
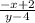
On cross multiplication,

2(y-4) = 3(-x+2)

2y-8 = -3x+6

3x+2y = 14.............equation(2)

Now, multiplying equation(1) by 2 and equation(2) by 3 and then equations are adding..

So, 4x-6y=36

9x+6y=42

________________

13x=78

x=6

Putting the value of x in equation(2)

18+2y=14

2y=-4

y=-2

So, coordinates of R(x,y) is R(6,-2).