Question

Line segment AB has endpoints A(1, 2) and B(5, 3). Find the coordinates of the point that divides the line segment directed from A to B in the ratio of 1:3.

A) (4, 2)
B) (3, 5/2)
C) (2/3, 2)
D) (2, 9/4)

Answer 1

Now despite what you may think, 1:3 is not 1/3 in this situation, but rather it's "1 equal part to 3 equal parts", which is a total of 4 equal parts. In short, they want the point that is at the 1/4 mark from A to B.

Firstly, how many units apart is 1 to 5 (the x-coordinates)? That would be 4 units apart. Multiply 1/4 by 4:

`(1)/(4)* (4)/(1)=(4)/(4)=1`

Next, how many units apart is 2 to 3 (the y-coordinates)? That would be 1 unit apart. Multiply 1/4 by 1:

`(1)/(4)* (1)/(1)=(1)/(4)`

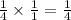
Next, since from 1 to 5 you are increasing, add 1 to 1.

`1+1=2`

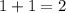
2 is the x-coordinate of the new point.

Next, since from 2 to 3 you are increasing, add 1/4 to 2.

`2+(1)/(4)=2(1)/(4)=(9)/(4)`

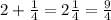
9/4 is the y-coordinate of the new point.

Putting it together, the point which divides AB into a 1:3 ratio is (2, 9/4), or D.