Question

Find the equation of the perpendicular bisector between A(-3,5) and A'(3,5)

Answer 1

a bisector of a line, is simply one line that cuts it into two equal halves.

we know the line is a bisector, for the segment A(-3,5) and A'(3,5), now, we could use the midpoint formula to get the midpoint, but there's no need, notice, the y-coordinate is the same for both, y = 5, meaning is just a horizontal line

`\bf \boxed{(-3,5)}\rule[0.35em]{10em}{0.25pt}\stackrel{\stackrel{midpoint}{\downarrow }}{(0,5)}\rule[0.35em]{10em}{0.25pt}\boxed{(3,5)}`

so the line must pass through 0,5.

now, we could find the slope AA', and since it's a horizontal line, we'd get a 0

`\bf (\stackrel{x_1}{-3}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{3}~,~\stackrel{y_2}{5}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{5-5}{3-(-3)}\implies \cfrac{5-5}{3+3}\implies \cfrac{0}{6}\implies 0`

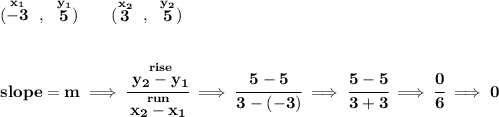
and get the negative reciprocal of that, for the slope of the perpendicular and so forth. However, there's no need, a perpendicular line to a horizontal line, is just a vertical line, so is really a vertical line passing through (0,5), so is right on the smack at the y-axis.

x = 0.