A proof by contradiction is one in which we assume the opposite of what we want to prove is true, and then explain how that assumption leads to a contradiction.
Here, we want to prove that the sum of an irrational number and a rational number is irrational, so we're going to assume the sum is rational and see why that can't possibly be true.
The question sets up this equation as a starting point:
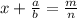
and we're told that a, b, m, and n are all integers. We can now subtract
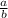 from both sides to get the equation in the form
from both sides to get the equation in the form
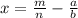
And here's where we run into our contradiction:
 , being the difference of two rational numbers, gives us a rational number as a result, but we also stated at the beginning that x was an irrational number. If we accept that, our equation now makes the absurd claim that
, being the difference of two rational numbers, gives us a rational number as a result, but we also stated at the beginning that x was an irrational number. If we accept that, our equation now makes the absurd claim that
irrational number = rational number
which is like saying that peanut butter = jelly, black = white, or up = down; it just doesn't make sense!
Since our reasoning was airtight, the only thing that could've led us down this tragic path was our assumption that the sum of an irrational and a rational number was rational, so we know now that the sum of a rational number and an irrational number must be irrational.