Answer:
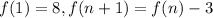
Explanation:
The given choices are
- f(1) = 8, f(n + 1) = f(n) + 3; for n _ 1
- f(1) = 8, f(n + 1) = f(n) - 5; for n _ 1
- f(1) = 8, f(n + 1) = f(n) + 5; for n _ 1
- f(1) = 8, f(n + 1) = f(n) - 3; for n _ 1
The given sequence is 8, 5, 2, -1,...
Where the first term is 8, the difference is -3, because the sequence is decreasing.
The arithmetic sequence is defined as

Where
 and
and
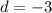 . So for a general term, the sequence is defined as
. So for a general term, the sequence is defined as
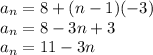
However, notice that the given choices are using another notation, which is an easier notation actually.
 refers to the first term of the sequence.
refers to the first term of the sequence.
We know that the difference is -3, that is, the sequence is made by adding -3 to the first term.
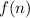 is the n-term and
is the n-term and
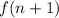 is the follwoing term.
is the follwoing term.
So, notice that to find the following term
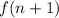 , we just need to add -3 to the first term
, we just need to add -3 to the first term
 .
.
Therefore, the function that best defines the sequence is
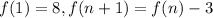
So, the right answer is the last choice.