Here are a few rules with exponents that apply here:
- Raising a power to a power:
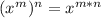
- Dividing exponents of the same base:
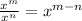
- Converting negative exponents to positive ones:

Firstly, solve the outer exponent:
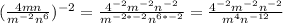
Next, divide:
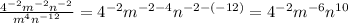
Next, convert the negative exponents:
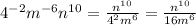
Your final answer is n^10/16m^6 , or B.