Question

An architect is designing a new building. He makes a model of the building such that the area of the rectangular base is 12x2 - 11x - 5 and the length is 3x + 1. The completed model will be in the shape of a rectangular prism where the volume is given by the polynomial 24x3 - 58x2 + 23x + 15. Determine the width and height of the model in terms of x. Fill in the values of m and b to complete the expressions. Type the width on the first line and the height on the second line

Answer 1

The general formula for the area of a rectangle is as follows, where l represents the length, and w represents the width.

The area of the rectangular base of the model is given by the polynomial 12x2 - 11x - 5. Since the length of the base is 3x + 1, use long division to find the width of the base as follows.

So, the width of the model's base is 4x - 5.

The general formula for the volume of a rectangular prism is as follows, where B represents the area of the base and h represents the height.

The volume of the completed model is given by the polynomial 24x3 - 58x2 + 23x + 15. Since the area of the base of the model is 12x2 - 11x - 5, use long division to find the height of the model as follows.

So, the height of the model is 2x - 3.

Explanation:

Answer 2

Since, the area of the rectangular base =
`12x^(2)-11x-5=0`

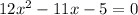
We have to determine the width if length is (3x+1)

Let us split the middle terms of the given equation to find its factors.

`12x^(2)-15x+4x-5=0`

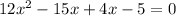
Taking common from first, second and third, fourth terms.

= 3x(4x-5)+1(4x-5)

= (3x+1) (4x-5)

Since, (3x+1) is the length of the rectangular base.

Therefore, the width of the rectangular base is (4x-5) units.

Now, Volume of the rectangular prism is given by the polynomial

`24x^(3)-58x^(2)+23x+15 = 0`

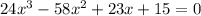
We have to find width and height.

Let x = -
`(1)/(3)` in the given equation of volume.

We get as,
`24(-(1)/(3))^(3)-58(-(1)/(3))^(2)+23(-(1)/(3))+15 = 0`

-135+135=0

Hence, (3x+1) is a factor of the given volume polynomial.

Now, performing long division of the given polynomial by (3x+1),

we get factors as (4x-5) and (2x-3).

So, the width is (4x-5) units and height is (2x-3) units.