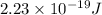The energy for vacancy formation
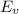 can be calculated as:
can be calculated as:
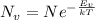
Here,
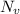 is equilibrium number of vacancies, N is number of atomic sites per unit vacancies, k is Boltzmann constant, T is temperature.
is equilibrium number of vacancies, N is number of atomic sites per unit vacancies, k is Boltzmann constant, T is temperature.
Here, number of atomic sites per unit vacancies can be calculated as follows:
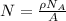
Here, ρ is density,
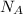 is Avogadro's number and A is atomic weight.
is Avogadro's number and A is atomic weight.
Putting the values,
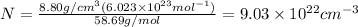
Converting
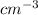 to
to

Since, 1
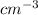 =
=
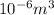
Thus,
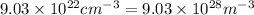
Now, the energy for vacancy formation
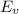 at 850 °C or 1123 K can be calculated using the following equation:
at 850 °C or 1123 K can be calculated using the following equation:
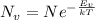
Rearranging,
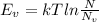
Putting the values,
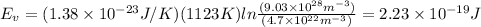
Therefore, energy for vacancy formation in nickel is