Question

A line’s slope is −16. The line passes through the point (6,2). Find an equation for this line in both slope-intercept form and point-slope form using the given point. An equation for this line in slope-intercept form is: . An equation for this line in point-slope form is:

Answer 1

Hello!

Here are how these forms are structured:

• Slope-intercept form: y = mx + b
• Point-slope form: y - y1 = m(x - x1)

In these forms, m is the slope, b is the y-intercept, and (x1, y1) is an ordered pair from the graph.

1. Slope-intercept form

To find the y-intercept, we have to substitute an ordered pair into the following equation: y = -16x + b, and solve for b.

2 = -16(6) + b

2 = -96 + b (add 96 to both sides)

98 = b

The slope-intercept form is y = -16x + 98

2. Point-slope form

Given a point from the graph and the slope, the equation will be very simple.

The point-slope form is y - 2 = -16(x - 6)

Final answers:

• Slope-intercept form: y = -16x + 98
• Point-slope form: y - 2 = -16(x - 6)

Answer 2

Slope-intercept form: y = -16x + 98

Point-slope form: y - 2 = -16(x-6)

Explanation:

Pre-Solving

We are given that a line has a slope (m) of -16 and passes through (6,2).

We want to find the equation of this line in slope-intercept form and point-slope form.

Slope-intercept form is given as y=mx+b, where m is the slope and b is the value of y at the y-intercept.

Point-slope form is given as
`y-y_1=m(x-x_1)` where m is the slope and
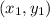`(x_1,y_1)` is a point.

Solving

Slope-intercept form

Let's start with slope-intercept form.

As we are already given the slope, we can plug that into the line.

Substitute -16 for m.

y = -16x + b

Now, we need to find b.

As the line passes through (6,2), we can use those values to solve for b.

Substitute 6 as x and 2 as y.

2 = -16(6) + b

2 = -96 + b

Add 96 to both sides.

98 = b

Substitute 98 as b into the equation.

y = -16x + 98

Point-slope form

Once again, we can substitute -16 as m into the equation.

We get:

`y-y_1=-16(x-x_1)`

Now, substitute 6 as
`x_1` and 2 as
`y_1`.

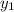y - 2 = -16(x-6)