Question

Average rate of change

Answer 1

In this problem, we have a table that shows living wages in Rochester. This study was made over a 5 year period. For a function of
`f`, the average rate of change can be found as follows:

`ARC=(f(x_(2))-f(x_(1)))/(x_(2)-x_(1))`

So, let's find the two ARC.

1. Average Rate of Change in the number of living wage jobs from 1997 to 1999:

In this item, we have that:

`x_(1)=1997 \\ x_(2)=1999 \\ \\ f(x_(1))=635 \\ f(x_(2))=745`

Therefore, the ARC is:

`ARC=(745-635)/(1999-1997) \\ \\ \therefore \boxed{ARC=55}`

So, from 1997 to 1999 the number of living wage jobs increases at a rate of 55 jobs per year

2. Average Rate of Change in the number of living wage jobs from 1999 to 2001:

In this item, we have that:

`x_(1)=1999 \\ x_(2)=2001 \\ \\ f(x_(1))=745 \\ f(x_(2))=800`

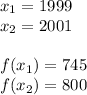
Therefore, the ARC is:

`ARC=(800-745)/(2001-1999) \\ \\ \therefore \boxed{ARC=27.5}`

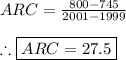
So, from 1999 to 2001 the number of living wage jobs increases at a rate of 27.5 jobs per year