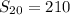Question

For the Rule of 78, for a 12-month period, the last term in the sequence is 12 and the series sums to 78. For an 10 month period, the last term is__ and the series sum is__ . For a 15 month period, the last term is __ and the series sum is . For a 20 month period, the last term is__ and the series sum is__ .

Answer 1

Answer:For the Rule of 78, for a 12-month period, the last term in the sequence is 12 and the series sums to 78. For an 10 month period, the last term is__ and the series sum is__ . For a 15 month period, the last term is __ and the series sum is . For a 20 month period, the last term is__ and the series sum is__ .

Explanation:

Answer 2

1) For an 10 month period, the last term is 10 and the series sum is 55.

2) For a 15 month period, the last term is 15 and the series sum is 120.

3) For a 20 month period, the last term is 20 and the series sum is 210.

Explanation:

Given : For the Rule of 78, for a 12-month period, the last term in the sequence is 12 and the series sums to 78.

To find :

1) For an 10 month period, the last term is__ and the series sum is__ .

2) For a 15 month period, the last term is __ and the series sum is .

3) For a 20 month period, the last term is__ and the series sum is__ .

Solution :

For the Rule of 78, for a 12 month period, the last term in the sequence is 12 and the series sums to 78. It is also defined as,

1+2+3+4+5+6+7+8+9+10+11+12=78

It is an AP with first term 1 and common difference 1.

The formula for sum of n terms is,

`S_n=(n)/(2)[a+l]`

Where, a is the first term and l is the last term

1) For an 10 month period, the last term is__ and the series sum is__ .

For an 10 month period, the last term is 10.

`S_(10)=(10)/(2)[1+10]`

`S_(10)=5[11]`

`S_(10)=55`

2) For a 15 month period, the last term is __ and the series sum is .

For an 15 month period, the last term is 15.

`S_(15)=(15)/(2)[1+15]`

`S_(15)=7.5[16]`

`S_(15)=120`

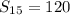
3) For a 20 month period, the last term is__ and the series sum is__ .

For an 20 month period, the last term is 20.

`S_(20)=(20)/(2)[1+20]`

`S_(20)=10[21]`

`S_(20)=210`