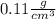Question

A cone has a mass of 6g and a radius of 5cm and a height of 2cm what is the density

Answer 1

Step
`1`

we know that

The density's formula is equal to

`density=(mass)/(volume)`

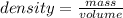
The volume of a cone is equal to

`Volume=(1)/(3)\pi r^(2) h`

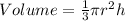
where

r is the radius of the base of the cone

h is the height of the cone

in this problem

`r=5cm\\ h=2 cm`

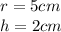
substitute the values in the formula above

`Volume=(1)/(3)*\pi*5^(2)*2`

`Volume=52.36\ cm^(3)`

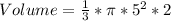
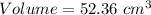
Step
`2`

Find the density

we have

`Volume=52.36\ cm^(3)`

`mass=6\ g`

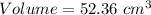
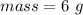
substitute in the formula

`density=(mass)/(volume)`

`density=(6)/(52.36)`

`density=0.11(g)/(cm^(3) )`

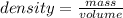
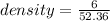
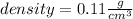
therefore

the answer is

the density is
`0.11(g)/(cm^(3) )`