Question

A cylindrical water tower has a height of 6 ft and a radius of 4 ft. How much water does the tower contain when it is 1/3 full? Approximate π as 3.14. Round your answer to the nearest tenth.

Answer 1

`\pi r ^(2) * h`

Answer 2

Water contains in the cylindrical water tower is 100.48 ft³ .

Explanation:

Formula

`Volume\ of\ a\ cylinder = \pi r^(2) h`

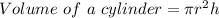
Where r is the radius and h is the height .

As given

A cylindrical water tower has a height of 6 ft and a radius of 4 ft.

π = 3.14

Putting all the values in the formula

`Volume\ of\ a\ cylinderical\ water\ tower =3.14* 4* 4* 6`

`Volume\ of\ a\ cylinderical\ water\ tower =301.44\ ft^(3)`

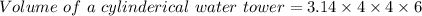
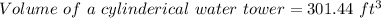
As given

`Tower\ contain\ water\ it\ is\ (1)/(3)\ full.`

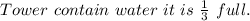
Thus

`Water\ contain\ in\ cylindrical\ tower = (1)/(3)* Volume\ of\ cylindrical\ water\ tower`

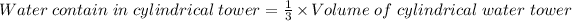
Putting values in the above

`Water\ contain\ in\ cylindrical\ tower = (1* 301.44)/(3)`

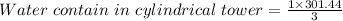
= 100.48 ft³

Therefore the water contains in the cylindrical water tower is 100.48 ft³ .