It represents a geometric sequence because it has a common ratio of 2.
In fact, a sequence is said to be geometric if any two adjacent elements are in the same ratio. In other words, if you choose any index
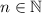 and consider the two consecutive terms
and consider the two consecutive terms
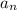 and
and
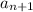 , you have
, you have
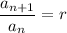
no matter which index you chose. In your case, the next term in the sequence is always the double of the previous one, so the ratio between two consecutive terms is always 2, and the series is geometric with common ratio 2